What is a Set in Mathematics?
A mathematical model for a collection of different things is called a set. A set has members or elements, which can be any mathematical object: variables, other sets, numbers, symbols, points in space, lines, other geometrical shapes, and variables. Curly brackets { } are typically used to represent sets; for instance, A = {1,3,5,7,9} is a set.
Similarly, in mathematics, the term "set" refers to a collection of objects whose components cannot be changed. To put it another way, the collection of data that does not pass from one person to another is what is meant to be called a set. The elements can be written in any order, but they cannot be repeated in the set.
Capital letters such as A, B, and C, are used to represent the set. Some types of sets include the infinite set, empty set, finite set, equivalent set, subset, universal set, and superset. During calculations, each kind of set has its own importance.
Which are the types of a Set in Mathematics?
There are several types of sets in Mathematics that are mentioned below.
- Disjoint Set
In Maths, two sets are supposed to be disjoint sets assuming that they share no component practically speaking. Two disjoint sets, on the other hand, are sets whose intersection is the empty set. For example, {1, 3, 5} and {7, 9, 11} are disjoint sets, while {0, 2, 4} and {4, 6, 8} are not disjoint.
- Empty or null Set
An invalid set or void set is a set that contains no components. It is indicated as ∅ = { }. For example, if we intersect set A= {1, 3, 5} with set B= {7, 9, 11}, the answer will be ∅ or { }.
- Equal Set
Sets can be equal to each other. If the sets are equal, they have the exact same elements in them. For example, set A= {a, b, c} and set B= {b, a, c} or set A= {1, 2, 3} and B= {1, 2, 3} are equal sets because they contain the number of elements.
- Equivalent Set
An equivalent set is essentially a set with an equivalent number of elements or members. The sets mustn't have similar members or elements, simply a similar number of elements or members. For example, set A= {a, b, c} and set B= {Apple, Banana, Carrot} or set A= {1, 2, 3} and B= {Pakisan, India, Bangladesh} are equal sets because they contain the equivalent number of elements or members.
- Finite Set
Finite (limited) sets will be sets having a limited/countable number of members or elements. For example , A = {1, 2, 3, 4, … ,100} or B = {a, b, c, d, … ,z} are the finite sets.
- Infinite Set
An infinite (endless) set is a set whose elements or members can not be counted. For example, A = {1, 2, 3, 4, … } or B = {a, b, c, d, … } are the limitless sets.
- Overlapping Set
Two sets A = {1, 2, 3, 4} and B = {4,5,6,7} are said to be overlapping because both sets A&B contain at least one element (4) in common. Overlapping sets are usually represented by using Euler Diagram.
- Singleton Set
In Mathematics, a singleton also called a unit set or one-point set is a set with precisely one element or member. For example, the set A = {3} is a singleton whose single element or member is {3}.
- Subset
Set A = {1,2,3} is supposed to be a subset of Set B = {1,2,3,4,5}if every one of the elements or members of Set A = {1,2,3} is likewise present in Set B = {1,2,3,4,5}. Similarly, we can also mean that set A is contained inside Set B. On the other hand, set A has {1,2,3} and set B has {1,2,3,4,5}, A is the subset of B since elements or members of A are likewise present in set B.- Unequal Set
Two sets A = {a,b,c,d,e} and B = {f,g,h,i,j} are supposed to be unequal sets because the elements or members of set A = {a,b,c,d,e} are absent in set B = {f,g,h,i,j} . Similarly, whenever, any two sets are not subsets of one another then the sets are called unequal sets.- Superset
In Mathematics, set A = {1,2,3,4,5} is considered as the superset of B = {1,2,3}, becaise all the members or elements of set B are also the members or elements of set A. Similarly, a superset is the complete opposite of a subset because in a subset we have reverse rule of superset.- Power Set
In Maths, the power set of a set A is the arrangement of all subsets of A, including the null or empty set and A itself. For example, If set A = {1, 2, 3} is a set, then all its subsets {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3} and ∅ are the members or elements of power set A, P(A) = { {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}, ∅} - Universal Set
In Mathematics, a Universal set is a set which contains all items, including itself. Similarly, in set theory as generally formed, it tends to be demonstrated in more ways than one that a Universal set doesn't exist. In any case, a few non-standard variations of set theory incorporate a general set. For example, set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is called a universal set.
What is the Union of Sets in Mathematics?
The association of any particular two or more sets is the sequential arrangement all the members or elements found in all the sets. For example, we have two different sets A = {1, 2, 3, 4, 5}and B = {6, 7, 8, 9, 10}. If we solve (union) them, the answer would be;
A = {1, 2, 3, 4, 5}
B = {6, 7, 8, 9, 10}
Solution:
A ∪ B = {1, 2, 3, 4, 5} ∪ {6, 7, 8, 9, 10}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} Answer
What is the Intersection of Sets in Mathematics?
In intersection of any particular two or more sets a common member(s) or element(s) is/are found in all the sets. For example, we have two different sets A = {a, b, c, d, e}and B = {a, e, i, o, u}. If we solve (interset) them, the answer would be;
A = {a,b,c,d,e}
B = {a,e,I,o,u}
Solution:
A ∩ B = {a,b,c,d,e} ∩ {a,e,i,o,u}
A ∩ B = {a,e} will be the answer because both {a,e} are the common mmbers/elements in sets A&B.
What is the Complement of Sets in Mathematics?
The complement any particular set is characterized as a set that contains the components present in the general (universal). In other words, complement of set is the opposite of an intersection set because in a complement set, we remove away the common members/elements that are found in both sets. Let's solve an example and learn it practically. if the universal set U = {1,2,3,4,5,6,7,8,9,10} and set A = {1,3,5,7,9}, then solve the A′.
Solution:
U = {1,2,3,4,5,6,7,8,9,10}
A = {1,3,5,7,9}
A′ = {1,2,3,4,5,6,7,8,9,10} - {1,3,5,7,9}
A′ = {2,4,6,8,10} Answer
What is the Cartesian product of Sets in Mathematics?
In Maths, the Cartesian product of any two sets (say A and B) denoted as A × B, is the arrangement of all arranged matches. In other words, we multiply one term (element or member) of set A with another term (element or member) of set B and hence make pair of them in a sequential order.
For example; if A = {1,2,3} and B = {a, b, c}, then the Cartesian Product of A and B, then find the Cartesian product.
Solution:
A = {1,2,3}
B = {a, b, c}
A × B = {1,2,3} × {a, b, c}
A × B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)} Answer
What is the Set-Builder Notation Form in Mathematics?
In set theory, the set-builder notation is a mathematical notation used to describe a set by representing its elements or explaining the properties that its members or elements must fulfill or satisfy.
For example;
The given integer (Z) set A = {..-4, -3, -2, -1, 0, 1, 2, 3, 4, 5} (Roster Form),
the set builder notation is A = {x ∈ Z | x ≤ 5} (Builder Form).
Note that; in set builder form symbol
"x" represents all the negative and positive members or members (-4, -3, -2, -1, 0, 1, 2, 3, 4, 5)
"∈" means "that belongs to" or "member(s) of"
" Z" symbol of the integer set
"|" means "such that"
"≤" means "less than or is equal to"
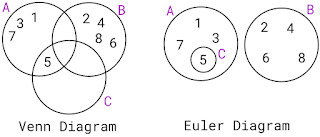
What is the Euler Diagram and Venn diagram of Sets in Mathematics?
An Euler diargam or chart is a realistic portrayal generally used to represent the connections between sets or gatherings; the outlines are normally drawn with circles or ovals, despite the fact that they can likewise utilize different shapes.
on the other hand, A Venn diagram or chart is an outline that utilizations circles to show the connections among things or limited gatherings of things. Circles that cross-over have a shared characteristic while circles that don't cover don't share those qualities. Venn diagram or chart helps to address the similiarities and contrasts between two or more sets in Mathematics.
.jpeg)
Comments